《现代密码学概论》期末复习笔记
《现代密码学概论》期末复习笔记
第二章 古典密码的演化
古典密码中,小写字母表示明文,大写字母表示密文。每个英文字母与 $0\sim 25$ 一一对应,不考虑其他字符。
仿射密码
- 移位密码:$c=(m+k)\pmod {26}$
- 仿射密码:$c=(km+b) \bmod 26$
- 解密:$m=k^{-1}(c-b) \bmod 26$
- $k$ 需要存在模 $26$ 的逆元,即 $(k,26)=1$。求逆元需要使用扩展欧几里得算法。
- 攻击:已知明文攻击(及更高级别攻击) / 频率攻击
- 改进:多表替换密码——Vigenere 密码:按 $k$ 个字母一组进行移位变化,密钥为长度为 $k$ 的向量。
- 频率攻击:先找到密钥长度,然后根据密钥长度,对于每一位进行词频分析。
e, h 的对应密文字符为 F, W,请求出该仿射密码的密钥。分组密码
PlayFair 密码:
密钥矩阵生成: 使用一个关键字(去除重复字母)来生成一个 $5\times 5$ 密钥矩阵。
例如,关键字
playfair生成的矩阵如下(备注:I和J视为同一字母,占同一个格子):P L A Y F I R B C D E G H K M N O Q S T U V W X Z
明文处理: 将要加密的明文分成两个字母一组:
- 如果两个字母在同一行/列,将它们分别替换为同一行/列中的下一个字母。
- 如果两个字母不在同一行也不在同一列,将它们替换为形成一个矩形的另外两个角的字母。
Hill 密码:
- 对于分组大小为 $k$ 进行加密,密钥为一个 $k\times k$ 的矩阵。
- 将明文分成长度为 $k$ 的明文分组,对于每个分组将其写成 $1\times k$ 的行向量,直接与密钥矩阵相乘得到密文。
- 解密即乘上密钥矩阵的逆(需复习线性代数相关)即可。(以上运算均在 $\mod 26$ 意义下进行)
Friday 所对应的密文为 PQCFKU,求密钥 $K$。第三章 数据加密标准 DES
Feistel 体制
- 单轮 Feistel:
- 输入 64bit 的明文,分为长度为 32bit 的两部分 $L_i,R_i$
- Feistel 操作如下:$L_i=R_{i-1},~~R_i=L_{i-1}\oplus f(R_{i-1},K_i)$
- 多轮 Feistel:
- 进行多次(对于DES:16次)单轮 Feistel
- 最后输出 $R_nL_n$
- 证明:Feistel 加解密同结构:
- 令 $L_0’=R_n, ~R_0’=L_n$
- $L_1’=R_{0}’=L_n=R_{n-1}$
- $R_1’=L_0’\oplus f(R_0’,K_n)=R_n\oplus f(L_n,K_n)=(L_{n-1}\oplus f(R_{n-1},K_n))\oplus f(R_{n-1},K_n)=L_{n-1}$
- 即 $L_1’R_1’=R_{n-1}L_{n-1}$
- 同理可归纳证得 $L_i’R_i’=R_{n-i}L_{n-i}$,即加解密同结构
轮函数 F
- E 扩展:将 32bit $R_{i-1}$ 通过 E 盒 扩展至 48 bit。
- 密钥加:将扩展后的 $R_{i-1}$ 与 48bit 的轮密钥 $K_i$ 进行异或加。
- S 盒代换:将 48bit 分成 8 组,每组 6bit;通过 S 盒代换,将 6bit 压缩至 4bit,得到 32bit 的比特串。
- S 盒代换:第一位和最后一位作为行号,中间四位作为列号,进行代换
- S 盒具体定义如下:
- P 盒置换:将得到的 32bit 串通过 P 盒置换,得到 $R_i$。
DES 算法
- 初始经过 IP 置换
- IP置换、P置换、E置换等均为查表:$A_i’=A_{tab_i}$
- 进行 16 轮 Feistel 迭代
- 最后经过 IP 逆置换
- $IP[IP^{-1}[i]]=i$
密钥扩展
根据密钥 $K$ (56 bit)获得每轮的子密钥 $K_i$:
- 将 $K_{i-1}$ 经过 PC-1 选择置换(不改变长度)。
- 拆分成 $C_{i-1},D_{i-1}$ 各 28bit,分别进行循环左移 $LS_i$ 位。
- $LS_i$ 根据轮次决定。
- 对于 $i=1,2,9,16$:$LS_i=1$;其余 $LS_i=2$。
- 将得到的 $C_{i},D_i$ 拼接,并经过 PC-2 选择置换,将 56 bit 压缩至 48 bit,得到 $K_i$。
扩散与混淆
- 扩散:使明文和密文的统计关系尽可能复杂。
- 实现方式:将明文的统计特性散布到密文中,使明文的每一位影响密文的多位。
- DES 中对应:P 置换。
- 混淆:使密文的统计特性和密钥的取值变得尽可能复杂。
- DES 中对应:S 盒混淆。
分组加密模式
- EBC 电码本模式:$C_i=E(K,P_i)$
- CBC 密码分组链接模式:
- 加密:$C_1=E(K,[P_1\oplus IV]),~~C_i=E(K,[P_i\oplus C_{i-1}])$
- 解密:$P_1=D(K,C_1)\oplus IV,~~P_i=D(K,C_i)\oplus C_{i-1}$
- 相比较 EBC,不同明文得到不同密文,且不易被攻击;但会造成错误传递。
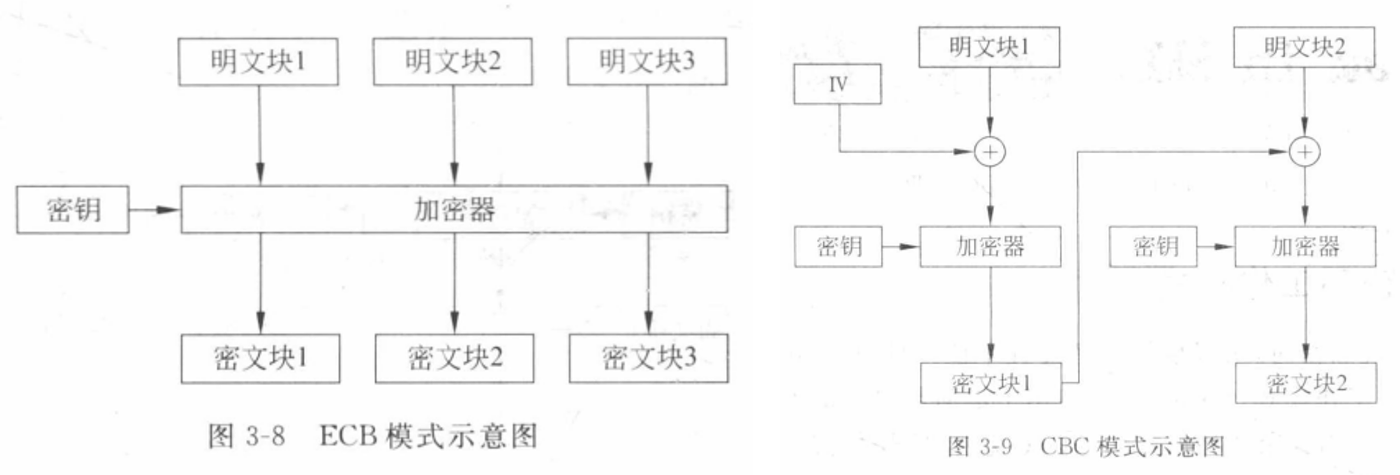
- CFB 密文反馈模式:
- 加密:
- $I_1=IV,~I_i=\text{Combine}(I_{i-1},C_{i-1})$
- $C_i=P_i\oplus E(K,I_i)$
- 解密:$P_i=C_i\oplus D(K,I_i)$
- 这里的 Combine 为移位寄存器左移一定位数后加上密文的值,下同。
- 加密:
- OFB 输出反馈模式
- 与 CFB 基本相同,区别为以 DES 输出代替密文:$I_i=\text{Combine}(I_{i-1},E(K,I_{i-1}))$。
- 相比 CFB,某一分组的密文传输出错,不影响其他组密文的解密,但难以消息流篡改攻击。
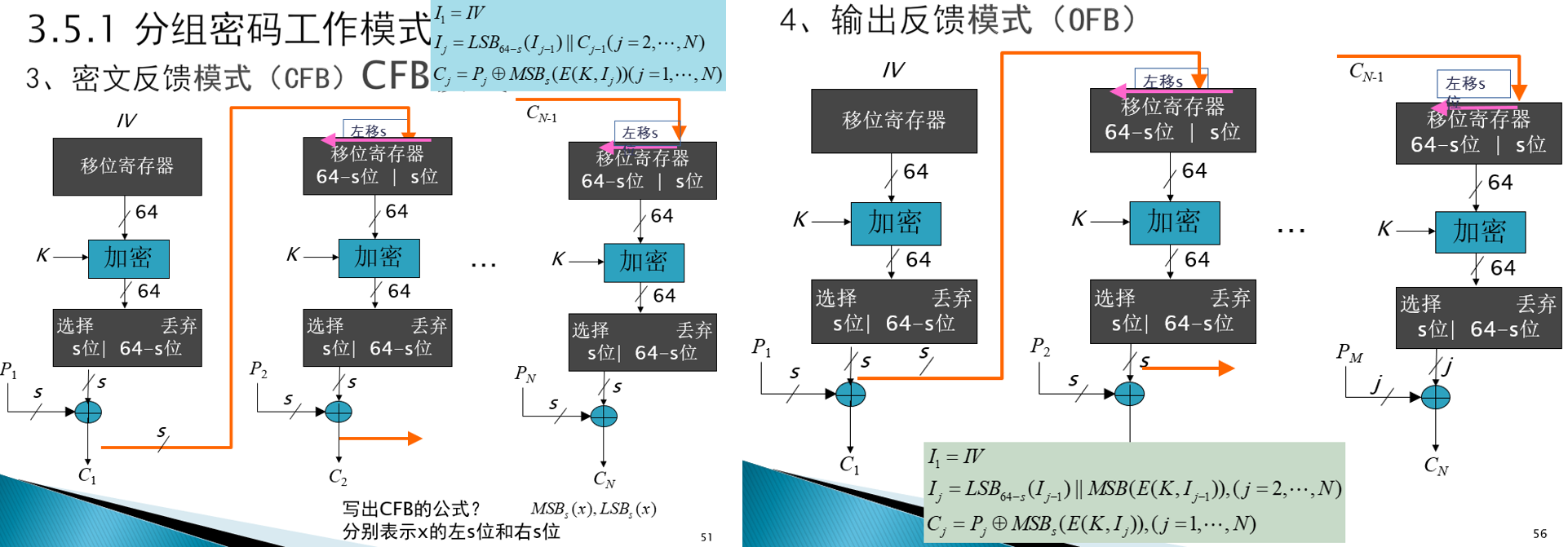
- CTR 计数器模式:
- $C_i=E(K,[P_i\oplus T_i])$,其中 $T_i$ 为计数器。
- 相比 CFB、OFB 可并行实现,效率更高,且没有错误传播;但可能被明文主动攻击(替换、重放)
第四章 高级加密标准 AES
AES 加密算法
分组加密对象:$128\text{bit}=16\text{bytes}$ 数据,从左到右填充 $4\times 4$ 的矩阵,称为 State 矩阵。
加密流程:
- 初始(第 0 轮)时进行轮密钥加。
- 轮密钥加:State 矩阵异或当前轮的密钥矩阵
- 进行 10 轮:字节代替、行移位、列混淆、轮密钥加
- 字节代替:给一个 $16\times 16$ 的 S 盒。对于 State 矩阵的每个字节,前 4 位为行号,后 4 位为列号,进行 S 盒替换。
- 行移位:对于 State 矩阵的第 $i$ 行循环左移 $i-1$ 位。
- 列混淆:State 矩阵乘上固定混淆矩阵。字节加、乘具体见后文。
- 轮密钥加
- 在最后一轮(第 10 轮),没有列混淆。
逆向解密:
- 初始时进行轮密钥加。这里和后面的轮密钥顺序与加密相反
- 进行 10 轮:逆向行移位、逆向字节代替、轮密钥加、逆向列混淆。
- 在最后一轮没有逆向列混淆。
密钥扩展
密钥以列为序进行排列。第 $n$ 轮的密钥即使用第 $n$ 组的密钥。
对于第 $n$ 组第 $i$ 列(其中 $i$ 不为 $0$),其密钥等于第 $n-1$ 组第 $i$ 列异或第 $n$ 组第 $i-1$ 列,即 $$ w_{n,i}=w_{n-1,i}\oplus w_{n,i-1}, ~(1\le i\le 3) $$
对于第 $n$ 组第 $0$ 列比较复杂:基于第 $n-1$ 组第 $3$ 列,先将其循环左移 1 个字节,然后对每个字节进行 S 盒替换,最后将第一个字节异或上 $RC_n$。将得到的结果 $g$ 异或上 $w_{n-1,0}$ 即为 $w_{n, 0}$
- $RC_i=2*RC_{i-1}$,运算定义在 $\text{GF}(2^8)$ 上
- $1\le i\le 8$:$RC_i=2^{i-1}$;$RC_9=\text{1B},RC_{10}=\text{36}$。
已知 AES 算法中密钥 $K=$ 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c
求:密钥编排算法输出的第一轮密钥 $K_4K_5K_6K_7$。
有限域运算
对于一个包含 8 个比特的字节,可以将其视为 $\text{GF}(2^8)$ 上的一个多项式,即 $$ f(x)\equiv a_7x^7+a_6x^6+\dots+a_1x+a_0\pmod{m(x)} $$ 可以由 8 个二进制系数 $(a_7a_6\dots a_0)$ 唯一表示,这样将 8 比特整数与 $\text{GF}(2^8)$ 上多项式一一映射,运算规则也直接使用有限域 $\text{GF}(2^8)$ 上的运算规则。
加法:不难发现等价于直接按位异或
乘法:(以 $m(x)=x^8+x^4+x^3+x+1$ 为多项式作为有限域)
引入 X 乘法: $$ x\times f(x) = b_6b_5b_4b_3b_2b_10~~~~~~~~~~~~~~~~~~~~~~~~~~~(b_7=0) $$
$$ x\times f(x) = b_6b_5b_4b_3b_2b_10\oplus(00011011)~~~(b_7=1) $$
推导:基于 $x^8\bmod m(x)=x^4+x^3+x+1$。
基于 X 乘法和 $f(x)\cdot x^n=(f(x)\cdot x^{n-1})\cdot x$,即可求解两个多项式之积。
第五章 RSA和公钥密码体制
公钥密码体制
公钥和私钥的对比:
| 保密性 | 加密算法中 | 数字签名算法中 | |
|---|---|---|---|
| 公钥 | 可以公开 | 用于加密信息 | 用于解密信息 |
| 私钥 | 必须保密 | 用于签名信息 | 用于验证签名 |
对称密码和公钥密码的对比:
| 对称密码 | 公钥密码 |
|---|---|
| 一个算法和一个密钥:加解密使用相同的算法和密钥 | 两个算法和两个密钥:加密算法使用公钥,解密算法使用私钥 |
| 发送方和接收方 事先确定算法和密钥 | 加密使用公钥,解密使用私钥。 |
| 密钥必须保密 | 私钥必须保密,而公钥公开 |
| 密钥管理困难,$n$ 个用户需要 $\frac{n(n-1)}{2}$ 对密钥 | 密钥管理相对简单,$n$ 个用户通信只要 $n$ 个公私钥对 |
| 无法实现数字签名 | 能实现数字签名 |
公钥密码体制显著特点:
已知密码算法和加密密钥,求解密密钥在计算上不可行。
基于数学函数(单项陷门函数),而非基于替换和置换。
RSA算法
- 私钥:$p,q,d$(大素数)
- 公钥:$n=p\times q, ~e$。易知 $\phi(n)=(p-1)(q-1)$。
- 计算私钥 $d$:$de\equiv1\pmod{\phi(n)}$
- 加密:$c\equiv m^e\pmod n$
- 解密:$m\equiv c^d\pmod n$
- 证明:由欧拉定理,$a^{\phi(n)}\equiv 1\pmod n$,可得 $m^e\equiv c^{de}\equiv c^{k\phi(n)+1}\equiv c\pmod n$。
RSA数字签名
- 签名:$sig\equiv m^d\pmod n$,发送 $(m,sig)$
- 验证:$sig^e\equiv m\pmod n$
- 若需要加密,加密传递为:先签名再加密
RSA攻击
选择密文攻击,即给定任意的密文 ${c_i}$ 可得到对应的 ${m_i}$。
- 攻击方式:对于 $c=m^e$,令 $c’=c\cdot x^e$,得到 $m’=(c\cdot x^e)^d=c^dx$,从而得到 $m’x^{-1}=c^d=m$。
明文攻击(e.g. 循环攻击,略)
共模攻击:若得到两个使用相同密钥 $n$ 的不同机构的明文密文对如下: $$ c_1\equiv m^{e_1}\pmod n\ c_2\equiv m^{e_2}\pmod n $$ 且 $(e_1,e_2)=1$,则根据扩展欧几里得算法,可解出 $s,t$ 使得 $se_1+te_2\equiv1\pmod n$。
故可以计算 $c_1^s+c_2^t\equiv m^{se_1+te_2}\equiv m\pmod n$。
设 RSA 加密体制的公钥是 $(e,n)=(77,221)$,用重复平方法加密明文 $160$,得到中间结果,如果攻击者得到以下中间结果就可以分解 $n$,请问攻击者如何分解 $n$?
| $i$ | 2 | 4 | 8 | 16 | 32 | 64 | 72 | 76 | 77 |
|---|---|---|---|---|---|---|---|---|---|
| $160^i\bmod 221$ | 185 | 191 | 16 | 35 | 120 | 35 | 118 | 217 | 23 |
第六章 离散对数加密算法
D-H密钥协商协议
- A 和 B 协商 $p,\alpha$,其中 $p$ 为质数,$\alpha$ 为 $p$ 的一个本原根。
- 设 A 的私钥为 $X_A$,B 的私钥为 $X_B$。
- A 计算公钥 $Y_A=\alpha^{X_A}$ 发送给 B,B 计算公钥 $Y_B=\alpha^{X_B}$ 发送给 A。
- A 计算密钥 $Y_B^{X_A}$,B 计算密钥 $Y_A^{X_B}$,显然结果均为 $k=\alpha^{X_AX_B}$。
- 发送加密信息:$c=mk=m\alpha^{X_AX_B}$。
- A 解密:$m=c\cdot Y_B^{-X_A}$,B 同理。
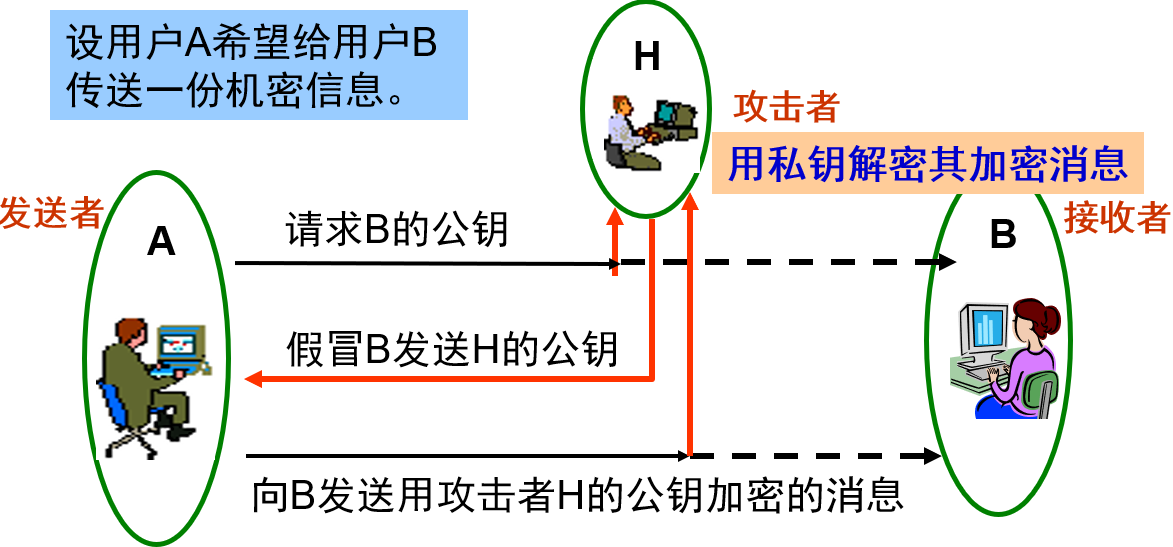
- 无法抵挡中间人攻击。
D-H 密钥协商协议中,素数 $q=11$,本原根 $\alpha=2$:
(1)用户 A 的公钥 $Y_A=9$,A 的私钥 $X_A$ 为多少?
(2)用户 B 的公钥 $Y_B=3$,A 与 B 协商的密钥 $K$ 是多少?
ElGamal 公钥体制算法
- 公钥: $p, \alpha,\beta=\alpha^x$,其中 $p$ 为质数,$\alpha$ 为 $p$ 的一个本原根。
- 私钥:$x$。
- 加密方选择随机数 $k$,发送 $(c_1,c_2)=(\alpha^k, \beta^km)$。
- 解密方解密:$m=c_2c_1\alpha^{-x}=\alpha^{xk}m\cdot \alpha^{-kx}$。
- 与 D-H 密钥协商协议的对比:
- 将解密方视为 A,加密方视为 B,则 $(X_A,Y_A)=(x,\alpha^x)$,$(X_B,Y_B)=(k,\alpha^k)$。
- 二者都是基于离散对数的难解性。
散列函数概述
哈希函数 $y=H(x)$ 的性质:
- 压缩性:将任意长度的输入值 $x$ 压缩成为固定长度的 Hash 值 $y$。
- 单向性:对于给定的 Hash 值 $y$,无法计算出输入值 $x$。
- 抗碰撞性:找不到不同的数据块对应相同的 Hash 值。
- 抗弱冲突(抗弱碰撞):对任意 $x$,寻找 $y(y\neq x)$,使得 $H(x)=H(y)$ 在计算上不可行;
- 抗强冲突(抗强碰撞):找到 $(x,y),x\neq y$,使得 $H(x)=H(y)$ 在计算上不可行。
哈希函数在密码学中的应用:
- 数据完整性校验(改变消息 $x$ 中任何一个或多个比特,都会使散列值发生变化,抗弱碰撞性保证 $h(x’)=h(x)$ 不成立)
- 数字签名(对发送的信息进行哈希,减小待签名信息的长度)
- 消息认证码(带密钥的 Hash 函数,可用于实现身份认证和消息认证)
DSA 数字签名算法
密钥生成过程:
- 选择两个质数 $p,q$,其中 $q|p-1$。
- 选择 $g$ 使得 $g\equiv\alpha^{\frac{p-1}{q}}\pmod p$($\alpha$ 为 $p$ 的本原根),则 $g$ 为模 $p$ 的阶为 $q$ 的元素。
- 选择私钥 $x\in (0,q-1)$,计算 $y\equiv g^x\pmod p$。
- 公布 $(p,q,g,y)$ 作为公钥。
生成签名:
- 选择随机数 $k\in(0,q-1)$。
- 计算 $r\equiv (g^k\bmod p)\pmod q$。
- 计算 $s\equiv k^{-1}(H(m)+xr)\pmod q$。
- 发送签名 $(r,s)$ 和消息 $m$。
验证签名:
- 计算 $u_1\equiv s^{-1}H(m)\pmod q, u_2\equiv s^{-1}r\pmod q$。
- 计算 $v\equiv (g^{u_1}y^{u_2}\bmod p)\pmod q$。
- 验证若 $v=r$,则签名有效。
第七章 密钥管理
密钥分配的基本方法(5种)
Alice 选取,通过物理手段传给 Bob(不安全/代价高)
可信第三方选取,通过物理手段传给 Alice 和 Bob(不安全/代价高)
Alice 和 Bob 事先已共享密钥 K,用 K 生成新密钥(一旦某次密钥泄露,之后密钥都不安全)
CA 为 Alice 和 Bob 选取密钥,并发送(对称密码体制的密钥分配)
Alice 和 Bob 在 CA 上发布自己的公钥(公钥密码体制的密钥分配)
对称密码体制的密钥分配
每一用户和 KDC 有一个共享密钥,称为主密钥(更贴切的是:密钥加密密钥)
KDC 通过主密钥(密钥加密密钥)分配给 Alice 和 Bob 的密钥是会话密钥。
通信完成后,会话密钥被销毁。
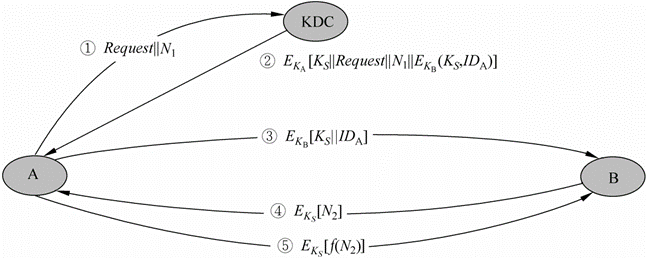
过程简单描述如下,具体过程见上图(其中 $N_1,N_2$ 为随机数):
- A 告诉 KDC 自己想和 B 通信,向 KDC 请求会话密钥。
- KDC 将会话密钥 $K_S$ 发送给 A。用 $K_A$ 加密以证明自己身份。
- A 将 KDC 用 $K_B$ 加密的会话密钥和自己的身份发送给 B。
- B 确认后向 A 验证其是否知道会话密钥。
- A 向 B 证明自己知道会话密钥。
公钥密码体制的密钥分配:Merkle密钥分配协议
分配过程:
A 有公私钥对 ${PK_A,SK_A}$,A 将公钥及身份 $(PK_A||ID_A)$ 发给B。
B 产生会话密钥 $K_S$,用 A 的公钥 $PK_A$ 加密,并发给 A。
A 由私钥 $SK_A$ 解密,恢复会话密钥 $K_S$。
缺点:不能抵抗中间人攻击:
- 敌手 E,其公私钥对 ${PK_E,SK_E}$:
- E 截获 A 向 B 发送公钥与身份 $(PK_A||ID_A)$ 后,将 $(PK_E||ID_A)$ 发送给 B。
- B 产生会话密钥 $K_S$ 后,用 $PK_E$ 加密 $K_S$ 发送给 A。
- $E_{PK_E}[K_S]$ 只有 E 能够由 $D_{SK_E}[E_{PK_E}[K_S]]$ 解密。
Merkle 协议抵抗中间人攻击方法(假设 A、B 已经交换公钥):
- A 和 B 先验证对方身份。
- A 用 $PK_B$ 加密 $ID_A$ 和随机数 $N_1$ 发往 B。
- B 用 $PK_A$ 加密 $N_1$ 和新随机数 $N_2$ 发往 A;B 成功解密使得 A 确认 B 的身份。
- A 用 $PK_B$ 加密 $N_2$ 发往 B;A 成功解密使得 B 确认 A 的身份。
- A 向 B 发送 $M=E_{PK_B}[E_{SK_A}[K_S]]$,B 使用 $SK_B,PK_A$ 解密后得到 $K_S$。
- 保证只有 A 能发送,B 能解读。
第八章
Shamir 门限方案
$(t, w)$ 门限方案(秘密共享)
- 秘密 $M$ 被拆分成 $w$ 个份额 $S_1,S_2,\dots,S_w$
- 任意 $\ge t$ 个份额可以恢复出秘密 $M$
共享过程:
构造 $t-1$ 次多项式:$S(x)=M+a_1x+a_2x^2+\dots+a_{t-1}x^{t-1}$
秘密分割:计算 $S_i=S(i),i=1\sim w$
秘密恢复:给定 $t$ 个份额,使用拉格朗日插值法恢复秘密 $M$: $$ M=\sum_{i=1}^t S_i\prod_{j=1,j\neq i}^t \frac{-j}{i-j} $$
拉格朗日插值法恢复多项式公式如下,求 $M$ 实际就是将 $x=0$ 带入 $$ S(x)=\sum_{i=1}^t S_i\prod_{j=1,j\neq i}^t \frac{x-j}{i-j} $$
零知识证明
以离散对数问题为例:证明方需要向验证方证明自己知道 $y=g^x$ 的离散对数 $x$。
- 交互式零知识证明:
- 证明方随机生成整数 $t$,并将 $R=g^t$ 发送给验证方;
- 验证方生成随机数 $u$,发送给证明方;
- 证明方将 $w=t-ux$ 发送给验证方;
- 验证方验证 $g^wy^u$ 是否等于 $R$。
- 非交互式零知识证明:
- 证明方直接生成 $u=H(y,R)$,然后将 $R,w$ 一次性发送给验证方进行验证。
第九章 椭圆曲线
定义
有限域 $\mathbb F$ 上的椭圆曲线 $E$: $$ y^2\equiv x^3+ax+b\pmod p $$ 记作 $E_p(a,b)$。
求椭圆曲线上所有点:对每个 $x$ 计算 $x^3+ax+b$,若其模 $p$ 有二次剩余则求之。
加法运算
已知 $P(x,y)$,则 $-P(x,-y)$。
已知 $P(x_1,y_1),Q(x_2,y_2)$,求 $R(x_3,y_3)=P+Q$: $$ x_3\equiv \lambda^2-x_1-x_2\ y_3\equiv \lambda(x_1-x_3)-y_1 $$ $\lambda$ 计算:
计算 $P\neq Q$: $$ \lambda\equiv \frac{y_2-y_1}{x_2-x_1} $$
计算 $2P$:
$$ \lambda\equiv \frac{3x^2+a}{2y} $$
椭圆曲线密码算法
椭圆曲线群中的离散对数问题困难:已知 $E_p(a,b)$ 中的元素 $Q$ 和 $R$,求方程:$R=xQ$ 中 $x$ 的值困难。
椭圆曲线密码算法类比 ElGamal 加密算法,定义在椭圆曲线 $E_p(a,b)$ 上:
- 公钥:$G,\beta=xG$,其中 $G$ 为生成元
- 私钥:$x$
- 加密:发送 $(c_1,c_2)=(kG,k\beta+m)$
- 解密:$m=c_2-xc_1=kxG+m-kxG$
利用椭圆曲线实现 ElGamal 密码体制,设椭圆曲线是 $E_{11}(1,6)$ ,生成元 $G=(2,7)$,接收方 A 的私钥为 $n_A=7$:
(1) 求 A 的公钥 $P_A$ ;
(2) 发送的消息为 $m=(10,9)$,选择随机数 $k=3$,求密文 $C$。
基于椭圆曲线的密钥协商协议
类比 D-H 密钥协商协议,实现椭圆曲线离散对数困难问题的密钥协商协议:
- A 和 B 协商 $E_p(a,b),G$,其中 $G$ 为生成元。
- 设 A 的私钥为 $X_A$,B 的私钥为 $X_B$。
- A 计算公钥 $Y_A=X_AG$ 发送给 B,B 计算公钥 $Y_B=X_BG$ 发送给 A。
- A 计算密钥 $X_AY_B$,B 计算密钥 $X_BY_A$,显然结果均为 $k=X_AX_BG$。
- 发送加密信息:$c=m+k=m+X_AX_BG$。
- A 解密:$m=c-X_AY_B$,B 同理。